自分に向けた学習用のメモになります。
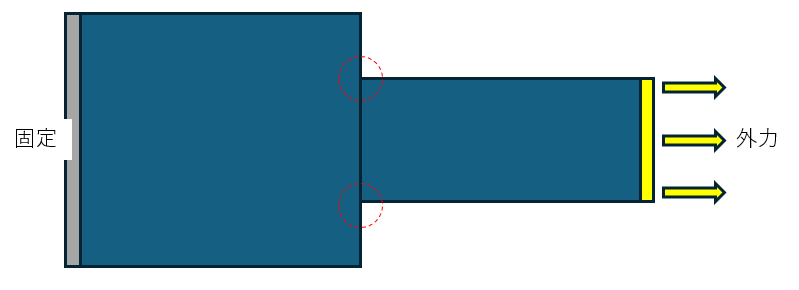
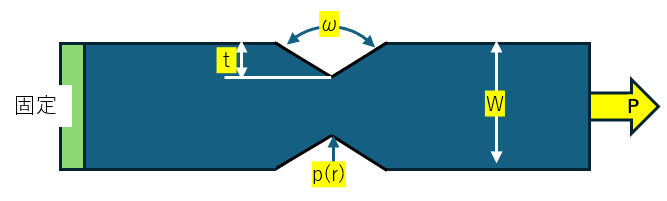
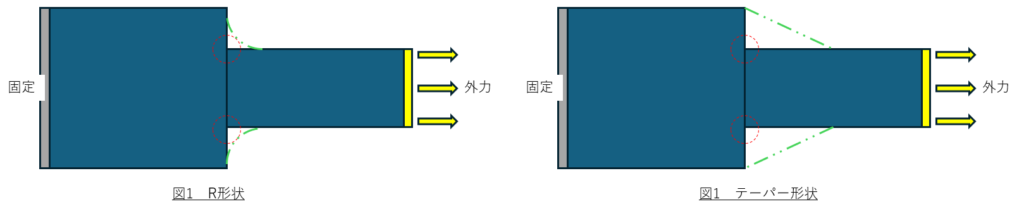
画像のような段付き板の形状の物体を矢印方向に引っ張った時、赤点線の隅部へ応力が集中する。その為、隅部の応力を均せるよう一般的な設計要領として、図1や図2のようにR形状をつけたりテーパー形状にする手法がよく用いられている。
個人的にやりたいこと
Rもテーパー角も大きければ大きい程いいと言われているが、ここの設定を机上で行いたい。
目的としては
- 解析前に予測を立てる
- 解析が必要かどうかの判断をする
- 説明を求められたときに答えれるようにしたい
といったところです。
応力集中の基礎
応力集中は形状の一様性が変化したときそこの部分の応力が局所的に大きくなること。
一般的に隅部は応力が集中しやすい。隅部への応力集中がどのくらいになるか机上で出すには応力集中係数を用いる。
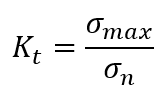
図3_応力集中係数の公式
応力集中係数(Kt)、最大応力(σmax)、公称応力(σn)
上記式の通り、応力集中係数を求めるには最大応力と公称応力が必要になる。
応力集中がどれくらいになるかを知りたいのに最大応力を入れる必要があり、結局解析しないと分からんのかい!という感じです。なので、応力集中係数や公称応力の式は実際の試験データを元に算出されており、それを使用する事になる。応力集中係数が分かれば、それに公称応力をかけてやれば最大応力を求めることが出来る。
【応力集中係数を知りたいとき】
この形状パターンの時は応力集中係数はコレで公称応力はコレ、みたいにまとめてある資料を探す。
応力集中係数一覧
自分が調べた中で見つけたもの
基準応力=公称応力
| 形状 | 基準応力σ0 | 応力集中係数α |
 円孔がある無限平板 | τ (せん断応力) | 4 |
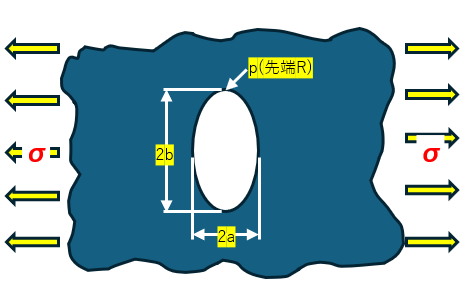 楕円孔がある無限平板 | σ (引張応力) | 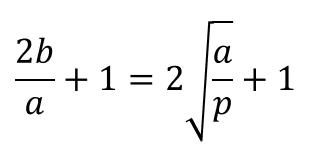 |
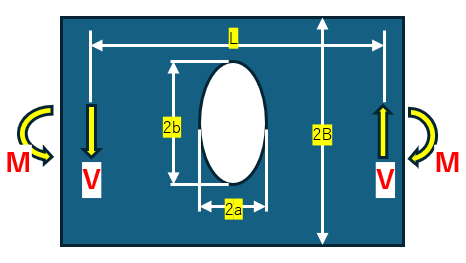 楕円孔がある有限平板 (無限箇所:左右)M=VL、t=板厚 | 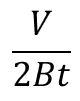 | 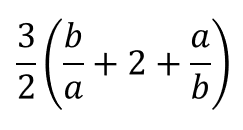 |
 半円切欠きをもつ半無限平板 (無限箇所:左右下) | σ (引張応力) | 2.76 |
その他の応力集中係数
形状の規格がある程度決まっている時の応力集中係数は、y=○○X4+○○X3+○○X2+○○X…といった多項式の形になり、次数も多く計算が複雑になる為excelなど計算ソフトで算出する。また、式をそのまま書くのは大変なのでグラフに変換し掲載されているところも多い。
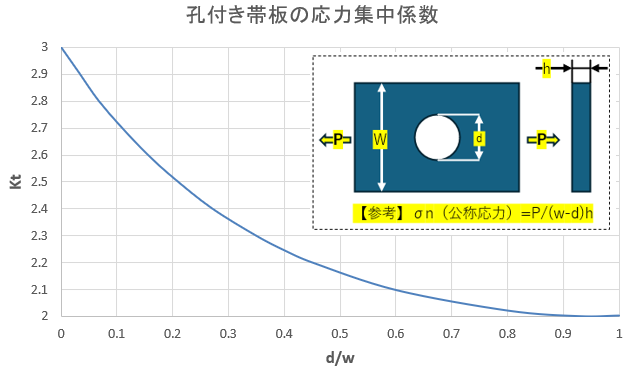
代表的な応力集中係数のグラフを作ってみた。簡単な形状でも一から計算するのは大変。似た形状のものでグラフを使って大体の係数を把握する、という使われ方が多いのかなと予想。excelがあれば計算は楽。
CAE解析をすると係数はどうなるか見てみた
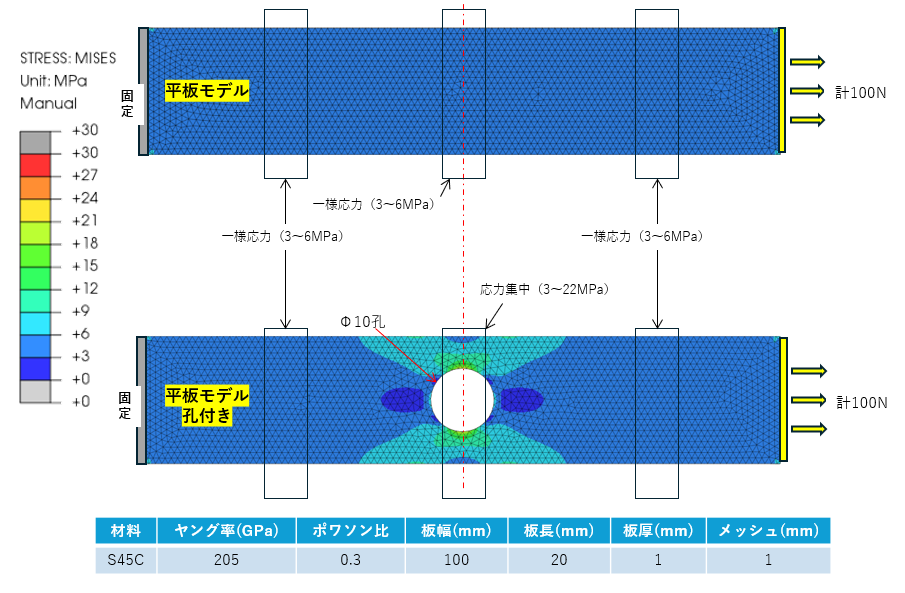
| P | W | d | h | 公称応力 (上のグラフの式) |
| 100N | 20mm | φ10 | 1mm | 10MPa |
公称応力が10MPaで最大応力が22MPaなので、応力集中係数は2.2という結果。
(公称応力=100/(20-10)*1)
これを上のグラフの式で見てみる。
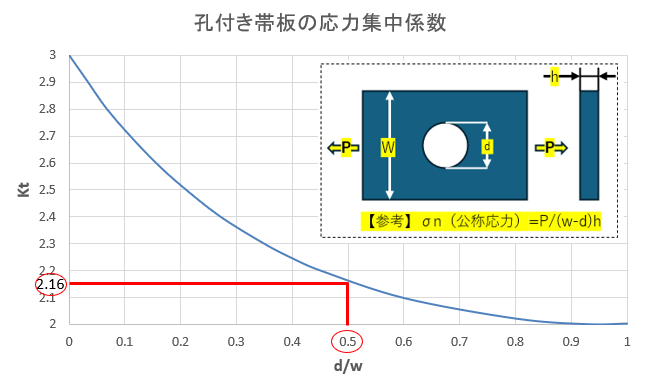
d/wは10/20で0.5…なので0.5の位置で見てみると2.16の位置。誤差は約1.8%。
なので、簡単な形状であれば机上計算でも目途付けとして十分使える認識。
検討に使いたい形状の応力集中係数を文献から探してくるのが結構大変なので、これが課題
切欠き形状の応力集中係数
個人的に一番しておきたいのは切欠き部の応力集中係数。
職場でもよく目にする形状。